An important SEO factor that is often overlooked on sites is the ALT text for an image. This is the text that describes what the image is about. If the image is not displayed this text will be shown. It is also used by screen readers for visially impaired users.
Used correctly, it is another opportunity to re-enforce the keyword of the page for the search engines and help improve the page keyword rankings.
But how can you easily see what the ALT text is for each image on a webpage? Web Text Analyzer makes this simple. Just enter the webpage URL, let it analyze the page and then view the ‘Image Details’ tab. This will then display all of the images on the page along with the ALT text for each image.
Here is an example of a site that has the ALT text setup and it is displayed correctly as text –
You can now look through this table and decide if each image has good and relevant ALT text set and edit the ALT text at the sites backend if necessary.
But if you have the ALT text set in the sites editor, how do you know Google can actually see it? Well you could go to Google Search Console for that site, run Fetch and Render and then check through the HTML code to find the ALT text for each image. A long process which is open to error.
Web Text Analyzer will tell you immediately. Here is an example of a site I have recently worked on. This is a Magento site and the product images all have ALT text added correctly in the editor. This show one of the images ALT text entries in the editor –
This is how Google sees the image. No ALT text! This can lead to big losses in Keyword rankings.
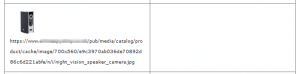
The problem here was down to a Magento image scroll function hiding the ALT text.
Without Web Text analyzer you would have no way of knowing that Google was not seeing the ALT text.
Related Post "Image ALT Text Detection"
